Gamme naturelle et gamme tempérée
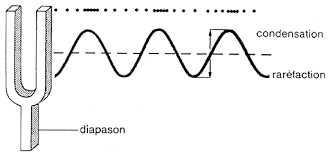
Quand nous chantons ou que nous jouons d’un instrument de musique, nous mettons l’air en vibration et c’est cette vibration que notre oreille perçoit. A chaque vibration, correspond une fréquence.
La note La au milieu du clavier du piano est aujourd’hui à la fréquence 440 hertz, soit 440 vibrations par seconde. (440 aller-retours de la corde autour de sa position d’équilibre)
On dit que l’être humain est capable d’entendre des sons entre 20 hertz et 16 000/20 000 hertz. Plus la fréquence est élevée, plus la note perçue est aigüe. Les notes du piano s’échelonnent par exemple entre 27.5 hertz pour le La le plus grave et 4 185,9 hertz pour le Do le plus haut. Le Si b aigu du biniou kozh est lui à près de 1870 hertz !
Lorsque l’on produit une note, par exemple un La à 440 hertz, cette fréquence est perçue mais également les fréquences suivantes : 880 (440×2), 1320 (440×3), 1760 (440×4) etc ….que l’on appelle les harmoniques. C’est un phénomène physique auquel on ne peut pas échapper. Chaque instrument de musique produit ses propres harmoniques, l’ensemble constituant ainsi le timbre de l’instrument. Ces harmoniques ont servi, dans l’histoire de la musique, à bâtir des gammes dites « naturelles ».
Pour comprendre plus facilement la construction de ces gammes, on va partir d’une note que l’on va appeler Do et à laquelle on va attribuer une fréquence théorique de 1.
Considérons maintenant une autre note à la fréquence 2. Lorsqu’elles sont produites simultanément, le résultat est plaisant à l’oreille, si plaisant que l’on va appeler la deuxième note du même nom que la première Do. On dit que la seconde note sonne à l’octave de la première.
Mais il faut plus de deux notes pour faire de la musique ! Il y a entre ces deux notes une note dont la fréquence est 3/2. C’est une note importante. On va l’appeler Sol. Si l’on joue cette note Sol à la fréquence 3/2, en même temps que la note Do à la fréquence 1, cela est également très plaisant à l’oreille. Pourquoi ? En raison des harmoniques. En effet, regardons les harmoniques produites par ces deux notes Do et Sol :
| Do fréquence 1 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | etc.. |
| Sol fréquence 3/2 | 3/2 | 2×3/2 =3 | 3×3/2=9/2 | 4×3/2=6 | 5×3/2=15/2 | 6×3/2=9 | 7×3/2=21/2 | etc… |
Et là on constate quelque chose de magique ! Plusieurs harmoniques sont communes aux deux notes : 3, 6, 9 etc. Cela explique qu’il y ait une consonance, un accord.
On peut faire le même exercice avec une note de fréquence 4/3 que l’on appellera Fa :
| Do fréquence 1 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | etc… |
| Fa fréquence 4/3 | 4/3 | 8/3 | 4 | 16/3 | 20/3 | 8 | 28/3 | 32/3 | ect… |
C’est ainsi qu’a été bâtie une des gammes « naturelles », basée sur des harmoniques, par le vénitien Giuseffo Zarlino (1517-1580 https://fr.wikipedia.org/wiki/Gioseffo_Zarlino). (nb : il existe d’autres gammes naturelles comme celle de Pythagore par exemple)
Voici ci- après la gamme de Zarlino :
| Note | Do | Ré | Mi | Fa | Sol | La | Si | Do |
| Fréquence | 1 | 9/8 | 5/4 | 4/3 | 3/2 | 5/3 | 15/8 | 2 |
Ou encore, si on l’exprime à partir d’un La à 440 hertz :
Tableau 1
| Note | Do | Ré | Mi | Fa | Sol | La | Si | Do |
| Fréquence Hertz | 264 | 297 | 330 | 352 | 396 | 440 | 495 | 528 |
Parmi ces notes, Do s’appelle la tonique et Sol, la dominante
Cette gamme a été utilisée en Occident jusqu’au XVII ème siècle. Elle est encore utilisée de nos jours dans la musique traditionnelle, par exemple avec la cornemuse écossaise où les notes du chanter viennent se marier, fusionner, avec le son continu des trois bourdons (un bourdon basse et deux ténors) et ce, grâce aux harmoniques !
C’est aussi le cas pour la musique bretonne traditionnelle qui est une musique modale avec la présence importante de la tonique (bourdons).
Pourtant, cette gamme naturelle a été délaissée à partir du XVIII ème siècle. Pourquoi ? En raison des gros problèmes rencontrés dès lors que l’on voulait faire jouer ensemble deux instruments de tonalités différentes comme par exemple un instrument en Do et un instrument en Ré.
| Notes | Do | Ré | Mi | etc |
| Instrument en Do | 1 | 9/8 | 5/4 | |
| Instrument en Ré | 9/8 | 9/8×9/8=81/64 |
Les Mi produits par les deux instruments n’ont pas exactement la même fréquence. Cela est dû au fait que les intervalles entre les notes ne sont pas réguliers. Reprenons notre instrument en Do :
| Note | Do | Ré | Mi | Fa | Sol | La | Si | Do |
| Fréquence | 1 | 9/8 | 5/4 | 4/3 | 3/2 | 5/3 | 15/8 | 2 |
Qu’est –ce qu’un intervalle entre deux notes, par exemple entre Ré et Mi ? Ce n’est pas la différence de leurs fréquences (5/4-9/8 = 1/8) mais le rapport entre leurs fréquences (5/4 : 9/8 soit 10/9). Là encore, c’est un phénomène physique : c’est le rapport entre les deux fréquences que perçoit l’oreille humaine.
On a alors les intervalles suivants entre les notes d’une gamme :
| Intervalle | Do-Ré | Ré-Mi | Mi-Fa | Fa-Sol | Sol-La | La-Si | Si-Do |
| Rapport de fréqences | 9/8 | 10/9 | 16/15 | 9/8 | 10/9 | 9/8 | 16/15 |
On voit bien par exemple que l’intervalle entre le Do et le Ré (9/8) n’est pas tout à fait le même que celui entre le Ré et le Mi (10/9)
C’est ainsi que l’on a décidé, afin de permettre à des instruments de tonalités différentes de jouer ensemble (ou de changer de tonalité pendant un morceau de musique) de créer une autre gamme dite « Tempérée », dans laquelle les intervalles entre les notes seraient égaux. On a donc tout simplement divisé l’octave (1-2) en douze intervalles égaux (les demi-tons). Pour représenter dans l’écriture musicale ces demi-tons, on a introduit aussi les altérations dièse (#–> un demi-ton au dessus de la note) et bémol (b–> un demi-ton en dessous de la note).
Par convention la gamme tempérée de Do s’écrit :
Do – Do# – Ré – Mib- Mi – Fa – Fa#- Sol – Lab – La-Sib – Do (gamme chromatique qui monte de 1/2 ton en ½ ton))
L’intervalle entre Do et Do# sera égal à celui entre Do# et Ré ou entre Ré et Mib.
Cela s’écrit :
Fréquence de Do#/fréquence de Do =Fréquence de Ré/Fréquence de Do#…..=fréquence de Do/fréquence de Si
Si on appelle R ce rapport (cet intervalle) constant, on aura bien R puissance12= 2 d’où R=1.0594631 entre chaque demi-ton (ou R²=1.059461×1.059461=1.1224621 entre chaque ton)
On a alors les nouveaux intervalles suivants :
| intervalle | Do-Ré | Ré-Mi | Mi-Fa | Fa-Sol | Sol-La | La-Si | Si-Do |
| rapport de fréquence | R²=1.1224621 | R² | R=1.0594631 | R² | R² | R² | R |
Ainsi, on va pouvoir calculer les fréquences des notes de la gamme tempérée de Do (gamme majeure diatonique) avec un La à 440 hertz
Tableau 2
| Note | Do | Ré | Mi | Fa | Sol | La | Si | Do |
| Fréquence | 261,63 | 293.66 | 329.63 | 349.23 | 391.99 | 440 | 493.88 | 523.26 |
Ainsi, voyez les petites différences pour les harmoniques suivantes qui ne sont pas ici parfaitement identiques, comme c’est le cas avec la gamme naturelle:
Harmoniques de Do : 261.63 x 3 = 784.89, 261.63 x 6 = 1569.78, 261.63 x 9 = 2354.67
Harmoniques de Sol : 391.99 x 2 = 783.98, 391.99 x 4 = 1567.96, 391.99 x 6 = 2351.94
On pourrait aussi calculer les fréquences des notes altérées et reconstituer ainsi toute la gamme chromatique.
Avec cette gamme on peut jouer dans un ensemble orchestral avec des instruments de tonalités différentes et changer de tonalité sans que cela pose de problème. On a en quelque sorte une gamme mathématique, que certains diront théorique, mais si pratique et si efficace qu’elle a permis le développement de la musique classique, à partir de Jean Sébastien Bach, puis contemporaine.
Mais, même si l’on est ici en gamme tempérée, il faut savoir que chaque note prise séparément conserve bien évidemment ses propres harmoniques (fréquences multipliées par 2, 3, 4, 5, 6, etc.) : c’est là une loi physique incontournable !
Et c’est ici le “hic”… On ne va pas retrouver la superposition exacte de certaines harmoniques de deux notes différentes jouées ensemble, comme par exemple le Do et le Sol, ainsi qu’on l’avait dans la gamme naturelle.
Ainsi, voyez les petites différences :
Do : 261.1 Hz 261.1 x 3 = 783.3 261.1 x 6 = 1566.6 261.1 x 9 = 2349.9 etc.
Sol : 392 Hz 392 x 2 = 784 392 x 4 = 1568 392 x 6 = 2352 etc.
C’est là le côté “imparfait” de la gamme tempérée
Pour être complet, voilà ci-dessous la gamme de Zarlino avec les fréquences des notes altérées
| Note | Do | Do# | Ré | Mib | Mi | Fa | Fa# | Sol | Lab | La | Sib | Si | Do |
| Fréquence | 1 | 16/15 | 9/8 | 6/5 | 5/4 | 4/3 | 45/32 | 3/2 | 8/5 | 5/3 | 16/9 | 15/8 | 2 |
YK Aout 2019
Annexe : Application à la cornemuse écossaise
Supposons une cornemuse dont le Si bémol grave est identique au Si bémol du piano pour lequel la référence est un La à 440 hertz. Alors, la fréquence du Si bémol , plus haut d’un demi-ton, est à 466,16 hertz (440 x 1.0594631)
Ici, le Sib grave est la tonique et le Fa la dominante (l’intervalle Sib grave-Fa s’appelle la quinte)
On aura donc les fréquences suivantes : (gamme naturelle)
| Note | Lab grave | Sib grave | Do | Ré | Mib | Fa | Sol | Lab | Sib |
| Fréquence | 8/9 | 1 | 9/8 | 5/4 | 4/3 | 3/2 | 5/3 | 16/9 | 2 |
| Fréquence (Hertz) | 414.17 | 466.16 | 524.43 | 582.70 | 621.55 | 699.25 | 776.94 | 828.74 | 932.32 |
Cette gamme présente la particularité de posséder un demi-ton entre le Ré et le Mib et un demi-ton entre le Sol et le Lab. Cette gamme particulière porte le nom de gamme mixolydienne.
(Nb : sur certaines cornemuses le Lab est à 7/4 au lieu de 16/9 du Sib grave)
La gamme tempérée de Sib correspondant toujours à un La à 440 hertz est alors la suivante :
| Note | Lab grave | Sib grave | Do | Ré | Mib | Fa | Sol | Lab | Sib |
| Fréquence (Hertz) | 415.30 | 466.16 | 532.25 | 587.33 | 622.25 | 698.45 | 783.99 | 830.61 | 932.33 |
Dans la gamme naturelle harmonique, la seconde (Sib-Do), la quarte (Sib grave-Mi) et la quinte (Sib grave-Fa) sont très proches de celles de la gamme tempérée.
Il en va différemment pour la tierce majeure ( Sib grave– Ré), pour la sixte majeure (Sib grave-Sol) et la septième mineure (Sib grave-Lab)
Pour autant, une cornemuse peut-elle dans ces conditions jouer avec un instrument tempéré (piano, accordéon, saxophone etc…) en La 440 Hertz sans que cela ne chatouille trop l’oreille ? L’oreille peut-elle discerner ces différences d’intervalle ?
A voir… ou plutôt, à écouter !
YK Miz Here 2019